Binary Addition, Subraction,Multiplication,Division

Binary Addition

It is a key for binary subtraction, multiplication, division. There are four rules of binary addition.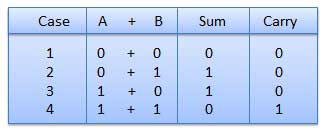
In fourth case, a binary addition is creating a sum of (1 + 1 = 10) i.e. 0 is written in the given column and a carry of 1 over to the next column.

Example − Addition

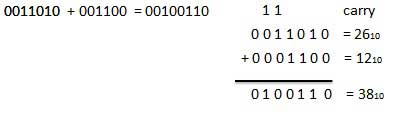
Binary Subtraction

Subtraction and Borrow, these two words will be used very frequently for the binary subtraction. There are four rules of binary subtraction.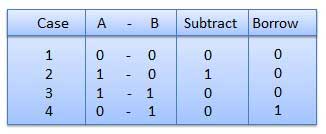

Example − Subtraction

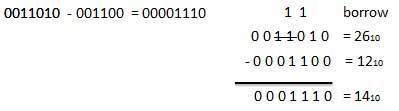
Rules of Binary Subtraction

• 0 - 0 = 0
• 0 - 1 = 1, and borrow 1 from the next more significant bit
• 1 - 0 = 1
• 1 - 1 = 0

For example,

00100101 - 00010001 = 00010100		0		borrows
		0  0  1 10  0  1  0  1	=	37(base 10)
		- 0  0  0  1  0  0  0  1	=	17(base 10)
		0  0  0  1  0  1  0  0	=	20(base 10)
00110011 - 00010110 = 00011101		0 10  1		borrows
		0  0  1  1  0 10  1  1	=	51(base 10)
		- 0  0  0  1  0  1  1  0	=	22(base 10)
		0  0  0  1  1  1  0  1	=	29(base 10)

Binary Multiplication

Binary multiplication is similar to decimal multiplication. It is simpler than decimal multiplication because only 0s and 1s are involved. There are four rules of binary multiplication.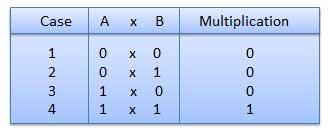

Example − Multiplication

Binary Division

Binary division is similar to decimal division. It is called as the long division procedure.

Example − Division

 Exercises

Binary Addition

**Reminder: 1 + 1 = 10**

Questions

1. 101 + 11 =
2. 111 + 111 =
3. 1010 + 1010 =
4. 11101 + 1010 =
5. 11111 + 11111 =

Binary Subtraction

**Reminder: 10 - 1 = 1**

Questions

6. 110 - 10 =
7. 101 - 11 =
8. 1001 - 11 =
9. 1101 - 11 =
10. 10001 - 100 =

Binary Multiplication

**Hint: very similar to decimal multiplication**

Questions

11. 10 x 10 =
12. 100 x 11 =
13. 101 x 10 =
14. 1011 x 11 =
15. 11011 x 101 =

Binary Division

**Hint: very similar to decimal division**

Questions

16. 100 / 10 =
17. 111 / 11 =
18. 1010 / 100 =
19. 1101 / 11 =
20. 10111 / 10 =