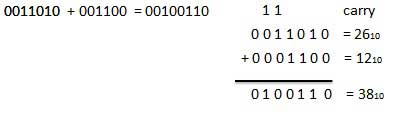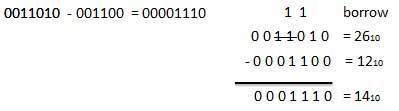Introduction: What is a Number System?
You probably already know what a number system is - ever hear of
binary numbers or hexadecimal numbers? Simply put, a number system is a
way to represent numbers.
We are used to using the base-10 number
system, which is also called decimal. Other common number systems
include base-16 (hexadecimal), base-8 (octal), and base-2 (binary).
In this article, I'll explain what these different systems are, how to work with them, and why knowing about them will help you.
Base-10 Mathematically
You may have noticed a pattern by now. Let's look at what is going on mathematically, using 2347 as an example.
- As you saw, there are 2 groups of a thousand. Not coincidentally,
1000 = 10*10*10 which can also be written as 103.
- There are 3 groups of a hundred. Again, not coincidentally,
100 = 10*10 or 102.
- There are 4 groups of ten, and,
10 = 101.
- Finally, there are 7 groups of one, and
1 = 100. (That may seem strange, but any number to the power of 0 equals 1, by definition.)
This is essentially the definition of base-10. To get a value of a
number in base-10, we simply follow that pattern. Here are a few more
examples:
892 = 8*102+9*101+2*1001147 = 1*103+1*102+4*101+7*10053 = 5*101+3*100
Admittedly, this all seems a little silly. We all know what value a
base-10 number is because we always use base-10, and it comes naturally
to us. As we'll see soon, though, if we understand the patterns in the
background of base-10, we can understand other bases better.
Binary to Octal and Octal to Binary Conversion
We know that binary and octal are two different kinds of number systems
whose bases are 2 and 8 respectively, i.e. they use 2 and 8 digits
respectively to represent their numbers and these numbers are 0, 1 (for
binary) and 0, 1, 2, 3, 4, 5, 6, 7 (for octal). Now we can transform any
numbers of these number system to other type of number system directly
without going through the decimal numbers. What is being tried to said
here that to transform a
binary number into octal number we can first convert it into decimal number and then convert that number into octal number or we can convert the binary number directly into
octal number, certainly the second method is more adaptable. This is also true for the reverse function, i.e. to transform an
octal number into binary number. The two methods are described in the following articles.
Binary to Octal
the binary numbers
are comprised of only 0 and 1 we have to first divide the binary number
into group of 3 digits starting from the right most side, and balancing
the number of digits by putting appropriate number of zeroes. Now we
have certain numbers of group of binary numbers, then we have to convert
those groups into decimal numbers and write in the same order in which
they used to be. Now this is the octal equivalent of that binary number.
If we consider an example, this will be very easy to understand.
Let us take a binary number say 101101001
2
Now dividing it into group of three digits we will find the following pattern
101|101|001
Now writing the equivalent decimal number of each group we get
5 | 5 | 1
So the equivalent octal number is 551
8
Octal to Binary Conversion
Now if we just imagine the reverse of the above explained operation we
will be able to find out the method for converting octal number into
binary number ourselves.
In this case each of the digits of the octal number is converted into
its equivalent binary number and they are merged into the same order
they were when they were as octal numbers, the leftmost zeroes are
omitted from the number and we get the equivalent binary number. An
example is given hereby to explain the method easily.
Let us take a number 34
8
Now the binary equivalent of 3 is 011 and that of 4 is 100.
So, the desired binary equivalent of the octal number is 111002.
Decimal to Octal Conversion
Any decimal number can be converted into octal number system by dividing it by the largest possible power of 8.
The remainder then again divided by the largest possible
power of 8, this method is repeated until the power of 8 is 1 and the
remainder obtained is less than 8. The result is obtained by arranging
the obtained quotients as they are acquired. The method will be clear by
a simple example Let us convert 13010 into octal number First of all we have to divide it by the largest possible power of 8 i.e. 82
130 / 8
2 = 2
130 - 8
2×2 = 2
2 / 8
1 = 0
2 - 0 = 2
2/8
0 = 2
So the octal equivalent of 130
10 is 202
8
Octal to Decimal Conversion
Similarly any octal number can be converted into decimal number. The
method is quite similar to the transformation of any binary number to
decimal number, the only difference is that in this case the 2 s will be
replaced by 8 and everything else i.e. the methods will remain same. So
it is quite clear if we want to change any octal number into decimal
number we have to start multiplying the digits of the number from right
hand side with increasing powers of 8 staring from 0 and finally summing
up all the products. The method will be clearer with an example.
Suppose we want to convert 1238 into decimal number, so we have to follow the procedure as shown below
123
8 = 1×8
2 + 2×8
1 + 3×8
0 = 64 + 16 + 3 = 73
So, the decimal equivalent of the number 123
8 is 73
10
Binary to Hexadecimal and Hex to Binary Conversion
As we are going through the basics of the digital electronics
the first and very important part is understanding the different types
of number system. As we have already discussed about the properties of
various number system and interrelation among some of them, now this is
the time to interrelate binary and hexadecimal number system. The
conversion from one number system is quite easy and we will discuss both
the cases in the following articles i.e. from
binary to hexadecimal and from
hexadecimal to binary conversion.
Binary to hexadecimal Conversion
To convert a
binary number to hexadecimal number first we have to divide the digits of the binary number
into groups of four taking from the right most side of the number and
in the last group the number of digits is made four by putting zeroes in
the left most side.
After that the groups are converted into decimal numbers
individually and written side by side in the same order as they were
previously, now we have got the desired equivalent hexadecimal number of
the binary number, an example will make it all clear for us.
We take any binary number suppose 100010100101
2
Breaking it into groups of 4 we get
1000|1010|0101
Now converting all the groups into decimal numbers individually we get
8 | 10 | 5
So the desired hexadecimal equivalent of the binary number 100010100101
2 is 8A5
16
Hexadecimal to Binary Conversion
Similarly the vice versa operation is also possible, i.e. we can convert
any hexadecimal number into its equivalent binary number directly
without any intermediate steps. The method is pretty easy, first of all
we have to convert every digit of the hexadecimal number into its
equivalent binary numbers (making every group a group of four by adding
0s to the left of the number). After all the digits are converted into
binary numbers they are merged according to their positions to make the
final binary number which is equivalent to the hexadecimal number is
obtained. Now we will try to understand the method with the help of an
example.
3DC16 is the hexadecimal number which we want to convert into binary. We
know D and C are equivalent to 13 and 12 respectively in decimal number
system.
Now converting each digit into its binary equivalent number we get
0011|1101|1100
Now merging all these groups binary numbers to make the final binary number we get 1111011100
2 which is the binary equivalence of the hexadecimal number 3DC
16
Hexadecimal to Decimal and Decimal to Hexadecimal Conversion
The hexadecimal system is a number system with base 16. This number system is greatly used by modern computer system.
We already know about the decimal number system, binary number system and octal number system.
Like those there is another number system called hexadecimal number
system. As the name suggests there are 16 symbols in this number system
starting from 0. Before explaining the number system we should know why
this number system came into existence. The natural tendency of human is
to use decimal number system because they are familiar with this as the
use of 0 is very easy and the operations are user friendly. And the
computer systems used binary systems earlier because there are only two
states on and off. But as the dependency on computer grew up and
different mathematical programs and different softwares needed to be
developed there came the need to develop a number system having base
larger than decimal and 16 was chosen because the bits, bytes are
multiples of it.
Now days this number system is used in HTML and CSS,
hexadecimal notations are used in them. This number system was first
used around 1956 in Bendix G-15 computer.
Now coming to the representation of
hexadecimal number system,
in this number system there are 16 basic digits by which all the
numbers can be represented, these are 0, 2, 3, 4, 5, 6, 7, 8, 9, A, B,
C, D, E, F the first 10 digits are similar to decimal number system but
the last 6 digits represent 10, 11, 12, 13, 14 and 15 respectively. Any
number in hexadecimal number system can be converted into numbers of
other number system very easily, the procedures are given in the next
article.
Here in the decimal system, we use symbol 1 and 0 side by side that is 10 to represent • • • • • • • • • • + •
That is nine plus one. After that we will have 11 then 12 and so on.
That means after nine or 9 we bring back first non - zero digit of
symbol that is 1 at left side and repeat all the symbols from 0 to 9 at
its right side to represent next ten higher numbers from ten to nineteen
(10 - 19). After 19 we put 2 at left and repeat again 0 to 9 to
represent next ten higher numbers from twenty to twenty nine (20 - 29).
Decimal number system
is very basic number system as ten symbols or digits are used in
different combinations to represent all the numbers, this system is said
to be of base ten (10). Now think about a number system where you are
told to use sixteen symbols instead of 10 symbols. Then what will be
your basic construction of the new number system ? For that first we
have to find out 16 symbols to represent the basic digits of that new
number system. We can create new series of symbols for that, but if we
do so it will be very much difficult to remember. That difficulty can be
solved if we use commonly used symbols for that purpose. So we can
simply use 0 to 9 of decimal system to represents first ten digits 0 to 9
of this new number system. But for other 6 higher digits there are no
symbols available in decimal system so we have to search for them from
some commonly used system. We can easily get them from our alphabetical
system that means we can use A, B, C, D, E and F as next 6 higher digits
(from 10 to 15) in this new number system. The system where total 16
basic digits are used is known as hexadecimal number system.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| A ⇒ | • | • | • | • | • | • | • | • | • | • |
|
|
|
|
|
| B ⇒ | • | • | • | • | • | • | • | • | • | • | • |
|
|
|
|
| C ⇒ | • | • | • | • | • | • | • | • | • | • | • | • |
|
|
|
| D ⇒ | • | • | • | • | • | • | • | • | • | • | • | • | • |
|
|
| E ⇒ | • | • | • | • | • | • | • | • | • | • | • | • | • | • |
|
| F ⇒ | • | • | • | • | • | • | • | • | • | • | • | • | • | • | • |
In hexadecimal system we use 16 symbols to represent all numbers. These
symbols are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F. After F
we use 10 for next higher number 16. Then next increment is 11 which
used to represent next natural number 17 and so on.
Hence in hexadecimal system just after F, the first digit becomes 1 and
second digit will repeat from 0 to F one by one to represent natural
numbers 16 to 31.
That means, 10 ⇒ 16, 11 ⇒ 17, 12 ⇒ 18, 13 ⇒ 19, 14 ⇒ 20, 15 ⇒ 21, 16 ⇒
22, 17 ⇒ 23, 18 ⇒ 24, 19 ⇒ 25, 1A ⇒ 26, 1B ⇒ 27, 1C ⇒ 28, 1D ⇒ 29, 1E ⇒
30, 1F ⇒ 31. After this the first digit will increase to 2 and again
second digit will repeat from 0 to F one by one to represent natural
numbers 32 to 47 and so on.
Decimal to Hexadecimal Conversion
As we have already stated in the previous articles on number systems
that all the number systems are inter related, so as the decimal and
hexadecimal numbers. Any number in decimal number system can be
converted into hexadecimal number system. The procedure is given below.
If we try to understand the procedure with an example and step by step then it will be easier and better for us.
Let us first take any decimal number suppose we have taken 75
10 and now we want to convert it into hexadecimal number, first we have to divide it by 16
75/16 = quotient 4, remainder 11
As the quotient is less than 16, we have to stop here and the equivalent hexadecimal number will be
4B
8 = 75
10
Now we will discuss the method for a slightly bigger number,
Suppose the number is 1693
10
Now we divide it by 16
1693/16 = quotient = 105, remainder = 13(D)
Now we have to divide the quotient again by 16 and see the result
105/16 = quotient = 6 remainder = 9
As the quotient is less than 16 the calculation part is completed and we can now directly write the result
1693
10 = 69D
16
So the decimal number has been converted into a hexadecimal number.From
above explanation it can be understood that, hexadecimal number is the
summation of products of different digit with their respective
multipliers. The multipliers are 16
0, 16
1, 16
2, ........from right hand side or list significant bit (LSB). Let's have an example 4D2 and this would be expressed as

If we divide decimal 1234 by 16, we will get 77 as quotient and 2 as
remainder. Then if we divide decimal 77 by 16, we will get 4 as quotient
and 13 or D as remainder. Now if we write side by side from last
quotient to first reminder we will get 4D2 which is hexadecimal or hex
equivalent of the number 1234.
Hexadecimal to Decimal Conversion
In a similar way any hexadecimal number can be converted into a decimal number. We will look into the process with an example.
But before beginning it should be made clear that before conversion of
hexadecimal number all the letters of the number should be taken as
their numerical values in decimal number system, i.e. if a digit in
hexadecimal number is A then we have to take it as 10, now an example
will make the whole procedure clear.
Let us take any hexadecimal number 45B1
16, we have to convert
it into decimal number, so starting from the right most digit we have
to start multiplying the digits with ascending power of 16 starting from
0.
So the taken number will be operated as
In this procedure any hexadecimal number can be converted into decimal number.
The
value hexadecimal number is determined by multiplying every digit of
the hex number by its respective multiplier. We start from LSB or right
most digit and multiply it with 16
0, then come to the next digit at left of LSB and multiply it with 16
1 and after that we come to the further left digit and multiply 16
2
with it. We continue this up to MSB or left most bit. The add all this
product and finally we get decimal equivalent of hexadecimal number.
This one of the easiest process of
hexadecimal to decimal conversion.
Think about the hex number 4D2. Here the least significant bit of the number is 2 so we will multiply that with 16
0 or 1. Then come to the next left digit that is D OR 13 and we will multiply it with 16
1 or 16. Lastly we will multiply the left most digit or MSB i.e. 4 with 16
2.
Now if we add these three terms, finally we will get the dedcimal
equivalent of the said hexadecimal number. This is what Hexadecimal to
Decimal Conversion
Hence,
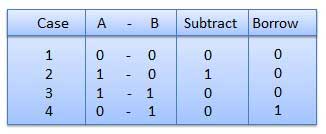
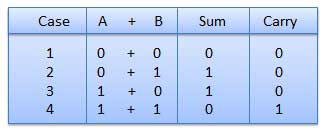 In fourth case, a binary addition is creating a sum of (1 + 1 = 10)
i.e. 0 is written in the given column and a carry of 1 over to the next
column.
In fourth case, a binary addition is creating a sum of (1 + 1 = 10)
i.e. 0 is written in the given column and a carry of 1 over to the next
column.