Matrices

Definition of Matrix

A matrix is a collection of numbers arranged into a fixed number of rows and columns. Usually the numbers are real numbers. In general, matrices can contain complex numbers but we won't see those
here. Here is an example of a matrix:

The upper left corner of the matrix is row 1 column 1. In the above matrix the element at row 1 col 1 is the value a1,1. The element at row 2 column 3 is the value a2,3.

Names for Matrices

If you sometimes forget whether rows or columns come first, just remember that matrices are build out of rowman columns. A matrix can be given a name. In printed text, the name for a matrix is usually a capital letter in bold face, like A or M. Sometimes as a reminder the dimensions are written to the right of the letter, as in B_3x3.
The elements of a matrix also have names, usually a lowercase letter the same as the matrix name, with the position of the element written as a subscript. So, for example, the 3x3 matrix A might be written as:

Sometimes you write A = [a_ij] to say that the elements of matrix A are named a_ij.

 

Square Matrix :
     Any matrix that has equal number of rows and columns is called square matrix. E.g: 2x2, 3x3 matrix.

2x2 Square Matrix		3x3 Square Matrix
a11 a12 a21 a22 2 rows & 2 columns		b11 b12 b13 b21 b22 b23 b31 b32 b33 3 rows & 3 columns

Diagonal Matrix :
     A Diagonal matrix is a square matrix with numbers on the leading diagonal and zeros in all other places.

Diagonal Matrix

2 0 0 0 3 0 0 0 8

Identity Matrix :
     An identity matrix is a square matrix denoted as I. It has ones (1) down the leading diagonal and zeros in all other places.

2x2 identity		3x3 identity
1 0 0 1		1 0 0 0 1 0 0 0 1

Note: Any matrix multiplied by its identity matrix leaves the matrix unchanged.
It is similar to multiplying a number by 1.

i.e AI = A (where A is a matrix)

2 2 5 3

x

1 0 0 1

=

2 2 5 3

Zero (Null) Matrix :
      A zero or null matrix is a matrix with 0 as the element for all its cells (rows and columns).

Zero (null) Matrix

0 0 0 0 0 0 0 0 0

Symmetric Matrix :
      A symmetric matrix is a matrix where a_ij = a_ji. i.e an element at the i^th row, j^th columns should be equal to the element at the j^th row, i^th columns.

Symmetric Matrix

1 2 3 2 4 5 3 5 6

Equality Matrix :
     For any two matrices to be said as equal matrices they should be of same size and have same values.

Matrix Equality

For two matrices to be equal, they must have

1. The same dimensions.
2. Corresponding elements must be equal.

In other words, say that A_{n x m} = [a_ij] and that B_{p x q} = [b_ij].
Then A = B if and only if n=p, m=q, and a_ij=b_ij for all i and j in range.
Here are two matrices which are not equal even though they have the same elements.

   

   

Matrix Addition

If two matrices have the same number of rows and same number of columns, then the matrix sum can be computed:

If A is an MxN matrix, and B is also an MxN matrix, then their sum is an MxN matrix formed by adding corresponding elements of A and B

Here is an example of this:
   

  Multiplication of a Matrix by a Scalar

A matrix can be multiplied by a scalar (by a real number) as follows:

To multiply a matrix by a scalar, multiply each element of the matrix by the scalar.

Here is an example of this. (In this example, the variable a is a scalar.)

Multiplying a Matrix by Another Matrix

But to multiply a matrix by another matrix you need to do the "dot product" of rows and columns ... what does that mean? Let me show you with an example:
To work out the answer for the 1st row and 1st column:

The "Dot Product" is where you multiply matching members, then sum up:

(1, 2, 3) • (7, 9, 11) = 1×7 + 2×9 + 3×11 = 58

We match the 1st members (1 and 7), multiply them, likewise for the 2nd members (2 and 9) and the 3rd members (3 and 11), and finally sum them up.

Want to see another example? Here it is for the 1st row and 2nd column:

(1, 2, 3) • (8, 10, 12) = 1×8 + 2×10 + 3×12 = 64

We can do the same thing for the 2nd row and 1st column:

(4, 5, 6) • (7, 9, 11) = 4×7 + 5×9 + 6×11 = 139

And for the 2nd row and 2nd column:

(4, 5, 6) • (8, 10, 12) = 4×8 + 5×10 + 6×12 = 154

And we get:

Matrix Subtraction

If A and B have the same number of rows and columns, then A - B is defined as A + (-B). Usually you think of this as:

To form A - B, from each element of A subtract the corresponding element of B.

Here is a partly finished example:

   

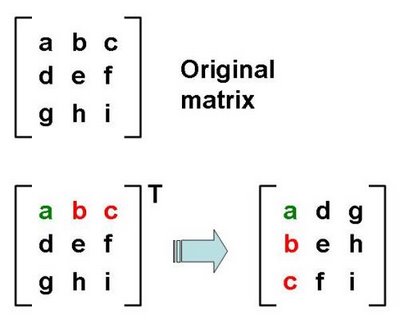
Transpose

The transpose of a matrix is a new matrix whose rows are the columns of the original (which makes its columns the rows of the original). Here is a matrix and its transpose:

The superscript "T" means "transpose". Another way to look at the transpose is that the element at row r column c in the original is placed at row c column r of the transpose. The element a_rc of the original matrix becomes element a_cr in the transposed matrix.
Usually we will work with square matrices, and it is usually square matrices that will be transposed. However, non-square matrices can be transposed, as well:

Rule for Transpose

If a transposed matrix is itself transposed, you get the original back:

This illustrates the rule (A^T)^T = A.

Determinant

The determinant of a matrix is a special number that can be calculated from the matrix. It tells us things about the matrix that are useful in system linear equations, in calculus and more.
The symbol for determinant is two vertical lines either side.

Example:

|A| means the determinant of the matrix A

Calculating the Determinant

First of all the matrix must be square (i.e. have the same number of rows as columns). Then it is just a matter of basic arithmetic. Here is how:

For  2×2 Matrix

For a 2×2 matrix (2 rows and 2 columns):

The determinant is:

|A| = ad - bc
"The determinant of A equals a times d minus b times c"

It is easy to remember when you think of a cross: Blue means positive (+ad), Red means negative (-bc)

Example:

|B|	= 4×8 - 6×3
	= 32-18
	= 14

For  3×3 Matrix

For a 3×3 matrix (3 rows and 3 columns):

The determinant is:

|A| = a(ei - fh) - b(di - fg) + c(dh - eg)
"The determinant of A equals ... etc"

It may look complicated, but there is a pattern:

To work out the determinant of a 3×3 matrix:

• Multiply a by the determinant of the 2×2 matrix that is not in a's row or column.
• Likewise for b, and for c
• Add them up, but remember that b has a negative sign!

As a formula (remember the vertical bars || mean "determinant of"):

"The determinant of A equals a times the determinant of ... etc"

Example:

|C|	= 6×(-2×7 - 5×8) - 1×(4×7 - 5×2) + 1×(4×8 - -2×2)
	= 6×(-54) - 1×(18) + 1×(36)
	= -306 Inverse of a Matrix using Minors, Cofactors and Adjoint You can calculate the Inverse of a Matrix by 1) calculating the Matrix of Minors, 2) then turn that into the Matrix of Cofactors, 3) then the Adjoint, and 4) multiply that by 1/Determinant. But it is best explained by working through an example! Example: find the Inverse of A: It needs 4 steps. It is all simple arithmetic but there is a lot of it, so try not to make a mistake! Step 1: Matrix of Minors The first step is to create a "Matrix of Minors": For each element of the matrix: ignore the values on the current row and column calculate the determinant of the remaining values Put those determinants into a matrix (the "Matrix of Minors") Determinants For a 2×2 matrix (2 rows and 2 columns) the determinant is easy: ad-bc Think of a cross: Blue means positive (+ad), Red means negative (-bc) The Calculations Here are the first two, and last two, calculations of the "Matrix of Minors" (notice how I ignore the values in the current row and columns, and calculate the determinant using the remaining values): And here is the calculation for the whole matrix: Step 2: Matrix of Cofactors This is easy! Just apply a "checkerboard" of minuses to the "Matrix of Minors". In other words, you need to change the sign of alternate cells, like this: Step 3: Adjoint (also called Adjugate) Now "Transpose" all elements of the previous matrix... in other words swap their positions over the diagonal (the diagonal stays the same): Step 4: Multiply by 1/Determinant Now find the determinant of the original matrix. This isn't too hard, because we already calculated the determinants of the smaller parts when we did "Matrix of Minors". So: multiply the top row elements by their matching "minor" determinants: Determinant = 3×2 - 0×2 + 2×2 = 10 And now multiply the Adjugate by 1/Determinant:   Inverse of a Matrix using Elementary Row Operations Also called the Gauss-Jordan method. This is a fun way to find the Inverse of a Matrix ... ... play around with the rows (adding, multiplying and swapping them) until you make your Matrix A into the Identity Matrix I. And by ALSO doing the changes to an Identity Matrix it magically turns into the Inverse! The "Elementary Row Operations" are simple things like adding rows, multiplying and swapping ... but let me show you with an example! Example: find the Inverse of "A": We start with the matrix A, and write it down with an Identity Matrix I next to it: (This is called the "Augmented Matrix") Identity Matrix The "Identity Matrix" is the matrix equivalent of the number "1": A 3x3 Identity Matrix It is "square" (has same number of rows as columns), It has 1s on the diagonal and 0s everywhere else. It's symbol is the capital letter I. Now we do our best to turn "A" (the Matrix on the left) into an Identity Matrix. The goal is to make Matrix A have 1s on the diagonal and 0s elsewhere (an Identity Matrix) ... and the right hand side comes along for the ride, with every operation being done on it as well. But we can only do these "Elementary Row Operations": swap rows multiply or divide each element in a a row by a constant replace a row by adding or subtracting a multiple of another row to it And we must do it to the whole row, like this: Start with A next to I In this example my first step was to add row 2 to row 1, then divide row 1 by 5, Then take 2 times the first row, and subtract it from the second row, Multiply second row by -1/2, Now swap the second and third row, Last, subtract the third row from the second row, And we are done! And matrix A has been made into an Identity Matrix ... ... and at the same time an Identity Matrix got made into A-1

Introduction to Sets

Introduction to Sets

What is a set? Well, simply put, it's a collection.

First you specify a common property among "things" (this word will be defined later) and then you gather up all the "things" that have this common property.

Notation

There is a fairly simple notation for sets. You simply list each element, separated by a comma, and then put some curly brackets around the whole thing.

The curly brackets { } are sometimes called "set brackets" or "braces".

Numerical Sets

So what does this have to do with mathematics? When we define a set, all we have to specify is a common characteristic. Who says we can't do so with numbers?

Set of even numbers: {..., -4, -2, 0, 2, 4, ...}
Set of odd numbers: {..., -3, -1, 1, 3, ...}
Set of prime numbers: {2, 3, 5, 7, 11, 13, 17, ...}
Positive multiples of 3 that are less than 10: {3, 6, 9}

Universal Set

At the start we used the word "things" in quotes. We call this the universal set. It's a set that contains everything. Well, not exactly everything. Everything that is relevant to the problem you have.

Equality

Two sets are equal if they have precisely the same members. Now, at first glance they may not seem equal, you may have to examine them closely!

Example: Are A and B equal where:

• A is the set whose members are the first four positive whole numbers
• B = {4, 2, 1, 3}

Let's check. They both contain 1. They both contain 2. And 3, And 4. And we have checked every element of both sets, so: Yes, they are!

And the equals sign (=) is used to show equality, so you would write:

A = B

Subsets

When we define a set, if we take pieces of that set, we can form what is called a subset.
So for example, we have the set {1, 2, 3, 4, 5}. A subset of this is {1, 2, 3}. Another subset is {3, 4} or even another, {1}. However, {1, 6} is not a subset, since it contains an element (6) which is not in the parent set. In general:

A is a subset of B if and only if every element of A is in B.

Proper Subsets

If we look at the definition of subsets and let our mind wander a bit, we come to a weird conclusion.
Let A be a set. Is every element in A an element in A? (Yes, I wrote that correctly.)

Well, yes of course, right?

So wouldn't that mean that A is a subset of A?
This doesn't seem very proper, does it? We want our subsets to be proper. So we introduce (what else but) proper subsets.
A is a proper subset of B if and only if every element in A is also in B, and there exists at least one element in B that is not in A.
This little piece at the end is only there to make sure that A is not a proper subset of itself. Otherwise, a proper subset is exactly the same as a normal subset.

Example:

{1, 2, 3} is a subset of {1, 2, 3}, but is not a proper subset of {1, 2, 3}.

Example:

{1, 2, 3} is a proper subset of {1, 2, 3, 4} because the element 4 is not in the first set.

You should notice that if A is a proper subset of B, then it is also a subset of B.

Empty (or Null) Set

  It is a set with no elements.This is known as the Empty Set (or Null Set). There aren't any elements in it. Not one. Zero. It is represented by Or by {} (a set with no elements) Some other examples of the empty set are the set of countries south of the south pole. So what's so weird about the empty set?

Order

No, not the order of the elements. In sets it does not matter what order the elements are in.

Example: {1,2,3,4) is the same set as {3,1,4,2}

When we say "order" in sets we mean the size of the set.

Just as there are finite and infinite sets, each has finite and infinite order.
For finite sets, we represent the order by a number, the number of elements.

Example, {10, 20, 30, 40} has an order of 4.

Table of set theory symbols

Symbol	Symbol Name	Meaning / definition	Example
{ }	set	a collection of elements	A={3,7,9,14}, B={9,14,28}
A ∩ B	intersection	objects that belong to set A and set B	A ∩ B = {9,14}
A ∪ B	union	objects that belong to set A or set B	A ∪ B = {3,7,9,14,28}
A ⊆ B	subset	subset has fewer elements or equal to the set	{9,14,28} ⊆ {9,14,28}
A ⊂ B	proper subset / strict subset	subset has fewer elements than the set	{9,14} ⊂ {9,14,28}
A ⊄ B	not subset	left set not a subset of right set	{9,66} ⊄ {9,14,28}
A ⊇ B	superset	set A has more elements or equal to the set B	{9,14,28} ⊇ {9,14,28}
A ⊃ B	proper superset / strict superset	set A has more elements than set B	{9,14,28} ⊃ {9,14}
A ⊅ B	not superset	set A is not a superset of set B	{9,14,28} ⊅ {9,66}
2A	power set	all subsets of A
Ƥ (A)	power set	all subsets of A
A = B	equality	both sets have the same members	A={3,9,14}, B={3,9,14}, A=B
Ac	complement	all the objects that do not belong to set A
A \ B	relative complement	objects that belong to A and not to B	A={3,9,14},     B={1,2,3}, A-B={9,14}
A - B	relative complement	objects that belong to A and not to B	A={3,9,14},     B={1,2,3}, A-B={9,14}
A ∆ B	symmetric difference	objects that belong to A or B but not to their intersection	A={3,9,14},     B={1,2,3}, A ∆ B={1,2,9,14}
A ⊖ B	symmetric difference	objects that belong to A or B but not to their intersection	A={3,9,14},     B={1,2,3}, A ⊖ B={1,2,9,14}
a∈A	element of	set membership	A={3,9,14}, 3 ∈ A
x∉A	not element of	no set membership	A={3,9,14}, 1 ∉ A
(a,b)	ordered pair	collection of 2 elements
A×B	Cartesian product	set of all ordered pairs from A and B
|A|	cardinality	the number of elements of set A	A={3,9,14}, |A|=3
#A	cardinality	the number of elements of set A	A={3,9,14}, #A=3
	aleph-null	infinite cardinality of natural numbers set
	aleph-one	cardinality of countable ordinal numbers set
Ø	empty set	Ø = { }	C = {Ø}
U	universal set	set of all possible values
ℕ0	natural numbers / whole numbers  set (with zero)	ℕ0 = {0,1,2,3,4,...}	0 ∈ ℕ0
ℕ1	natural numbers / whole numbers  set (without zero)	ℕ1 = {1,2,3,4,5,...}	6 ∈ ℕ1
ℤ	integer numbers set	ℤ = {...-3,-2,-1,0,1,2,3,...}	-6 ∈ ℤ
ℚ	rational numbers set	ℚ = {x | x=a/b, a,b∈ℕ}	2/6 ∈ ℚ
ℝ	real numbers set	ℝ = {x | -∞ < x <∞}	6.343434 ∈ ℝ
ℂ	complex numbers set	ℂ = {z | z=a+bi, -∞<a<∞,      -∞<b<∞}	6+2i ∈ ℂ

  
 Set-Builder Notation

venndiagrams

Venn Diagrams & Set Notation